During the running of the computer, due to various reasons, the data may be in error during the storage process. In order to detect the error in time and correct the error, the original data can usually be encoded into Hamming code.
Hamming code has a bit of error correction capability.
Parity is a way of adding a parity bit to indicate whether the previous data contains odd or even ones. If an odd number of bits have changed during the transfer, this error will be detected (note that the parity bit itself may also change). In general, if the data contains an odd number of 1, the parity bit is set to 1; conversely, if there is an even number of 1 in the data, the parity bit is set to 0. In other words, the new data consisting of raw data and parity will contain an even number of 1.
Parity is not always valid. If there are even bits in the data that change, the parity will still be correct, so no errors can be detected. Moreover, even if the parity detects an error, it cannot indicate which one has an error, making it difficult to correct. Data must be discarded and retransmitted as a whole. In a noisy medium, successfully transferring data can take a long time or even impossible. Although parity does not work well, it is the least expensive way to detect because it only requires one extra space overhead. Also, if you know the bit where the error occurred, the parity can also recover the data.
If a message contains more bits for error correction, and by properly arranging these error correction bits so that different error bits produce different error results, then we can find the error bit. In a 7-bit message, there are 7 possibilities for a single data bit error, so 3 error control bits are enough to determine if an error has occurred and which one has gone wrong.
Hamming coding scheme general algorithmThe following general algorithm can generate a Hamming code that can correct one bit for any digit.
First, the number of data bits (from left to right) starting with 1 is marked with the serial number, 1, 2, 3, 4, 5. .
2. Convert the position numbers of these data bits to binary, 1, 10, 11, 100, 101, and so on.
3. The position of the data bit in the sequence number is the power of the second power (numbers 1, 2, 4, 8, etc., that is, only one of the binary representations of the data bit position number) is the check digit.
Fourth, there are other positions of the data bits (at least 2 of the binary representation of the data bit position number is 1) is the data bit
5. Each bit of data is contained in a specific two or more check bits, which are determined by the binary representation of the position values ​​of these data bits.
1. Check digit 1 covers the binary representation of all data bit position numbers. The first digit of the last digit is 1: 1 (check digit itself, here is binary, the same below), 11, 101, 111, 1001, etc.
2. Check digit 2 covers the binary representation of all data bit position numbers. The second last digit is the data of 1: 10 (check digit itself), 11, 110, 111, 1010, 1011, etc.
3. Check digit 4 covers the binary representation of all data bit position numbers. The third digit is the data of the first digit: 100 (check digit itself), 101, 110, 111, 1100, 1101, 1110, 1111, etc.
4. Check digit 8 covers the binary representation of all data bit position numbers. The fourth digit of the last digit is 1: 1000 (check digit itself), 1001, 1010, 1011, 1100, 1101, 1110, 1111, etc.
5. In short, all check digits cover the data location and the number of binary AND values ​​of the check digit location that are not zero. It is feasible to use odd or even parity. Even parity is simpler from a mathematical point of view, but there is no difference in practice.
From the coding form, we can find that Hamming code is a very strict coding method. In this example, the verification and correction of the specific code bits is achieved by the combined detection of the 3 bits of the 4 data bits. (However, only one bit error is allowed, and two errors cannot be checked out. The following examples of error correction can be seen). In the verification, each Hamming code is added to the corresponding data bit value. If the result is even (the error correction code is 0), it is correct. If it is odd (the error correction code is 1), the current Hamming code is used. There is an error in the corresponding three data bits. At this time, the operation of each of the other two Hamming codes is used to determine which bit is a problem.
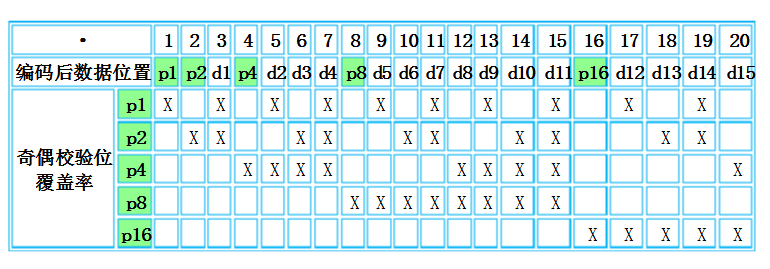
Observing the above table can find a relatively straightforward rule: the i-th check bit is the 2i-1th bit, starting from this bit, checking 2i-1 bits, skipping 2i-1 bits... and so on. For example, the third test bit p4 in the above table starts from the 23-1=4 position, and 4, 5, 6, and 7 are tested, and then 4, 8, 10, and 11 are skipped, and then 12, and then 12. 13, 14 and 15 total 4...
The encoding rules for Hamming codes are as follows:Fill in the new coded 2^(k - 1)( k "0" = 0) bit with 0 (ie check digit)
Put the rest of the new code into the original source
The parity bit is encoded in such a way that the k-th check code starts from the 2^(k - 1) bit of the new code, and each time an exclusive OR of 2^(k - 1) bits is calculated, jump 2^(k - 1) bit, then calculate the XOR of the next set of 2^(k - 1) bits, and fill in 2^(k - 1) bits, for example:
Bit 1 in the new check code encoding section 1 (2 ^ (1-1) == 1) (a Hamming code from the start), calculated 1,3,5,7,9,11,13, 15,. . . The XOR of the bit is filled in the first bit of the new code.
The second bit check code is located at the second bit of the new code (2^(2-1) == 2), and calculates 2,3,6,7,10,11,14,15. . . The XOR of the bit is filled in the second bit of the new code.
The third bit check code is located at the 4th bit of the new code (2^(3-1) == 4), and calculates 4,5,6,7,12,13,14,15,20,21,22, twenty three,. . . The XOR of the bit is filled in the 4th bit of the new code.
The 4th bit check code is located at the 8th bit of the new code (2^(4-1) == 8), and 8-15, 24-31, 40-47, is calculated. . . The XOR of the bit is filled in the 8th bit of the new code.
The fifth bit check code is located at the 16th bit of the new code (2^(5-1) == 16), and is calculated as 16-31, 48-63, 80-95. . . The XOR of the bit is filled in the 16th bit of the new code.
In mathematics, Hamming code is a binary linear code. For each integer m"2, there is one code with m parity bits 2m-m-1 data bits.
Hamming code generation and inspectionLet the binary code to be detected be n bits. In order to make it have error correction capability, it is necessary to add a detection bit of k bits to form a code of n+k bits. Then, the newly added detection digit k should satisfy:
2k≥n+k+1 or 2k-1≥n+k
When the number of bits of k is determined, they can be set according to the test task they are responsible for and their values ​​in the transmitted code. First, the code to be detected is divided into Pn groups, and how many groups are divided, we determine by the value of k. Below I use an example to illustrate.
Suppose the binary code to be detected is 0101, the number of bits is n=4. According to the formula 2k≥n+k+1, it can be concluded that the value of k is 3, so the final Hamming code should be n+k=7 bits.
Therefore, the grouping is divided into P1, P2, and P4. The first reason is the group 20, 21 is a second group, the third group 22 Similarly, sequentially pushed packet shall column 2k-1. At the same time, the position inserted according to the number generated by the grouping is also inserted according to this rule, for example, the first group insert 20, that is, the first bit, the second group insert 21, that is, the second bit, and so on. Then the components are good, and the bits they contain in each group are:
P1 contains (1,3,5,7,9,11,...)
P2 contains (2,3,6,7,10,11,14,15,...)
P3 contains (4,5,6,7,12,13,14,15,...)
How is the number contained in each group determined? Let's look at the table below.

Convert the number to binary from right to left, if the first digit is 1, for example the number is 1, 3, 5, 7. . . The first group is divided into 1, if the second digit is 1, for example number 2, 3, 6, 7, 10. . It is divided into the second group, and so on, all the numbers are assigned to the corresponding group. Let me see how the example 0101 generates the Hamming code (using the spouse principle).
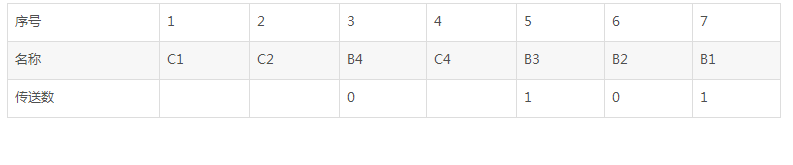
Where C1, C2, and C4 are the detection bits we inserted.
If Hamming code is configured according to the principle of spouse, C1 should make the number of "1" in 1 3 5 7 bits even; C2 should make the number of "1" in 2 3 6 7 bits even; C4 should make 4 The number of "1" in 5 6 7 bits is even.
According to what I said above:
C1=3 bits+5 bits+7 bits, ie C1=B4+B3+B1=0+1+1=0
C2=3 bits+6 bits+7 bits, ie C2=B4+B2+B1=0+0+1=1
C4=5 bits+6 bits+7 bits, ie C4=B3+B2+B1=1+0+1=0
Therefore, the Hamming code of 0101 should be C1C2B4C4B3B2B1, ie 0100101
Hamming code still has the principle of matching odds. Let's talk about the principle of matching odds. The Hamming code of 1100101 is configured according to the principle of matching.
According to 1100101, n=7 is known. According to the formula, we can find that we need to add k=4 bit detection bits. The details are as follows.

Configured according to the principle of matching, then
C1=3 bits+5 bits+7 bits+9 bits+11 bits+1=1+1+0+1+1+1=1
C2=3 bits+6 bits+7 bits+10 bits+11 bits+1+1
C4=5 digits+6 digits+7 digits +1=0
C8=9 digits+10 digits+11 digits+1+1
Therefore, the Hamming code newly configured according to the odd principle is 11101001101.
Hamming code verification error instanceLet's take the above code as an example. Suppose we have received the code 001101001. We can find that the 8th bit of the Hamming code is different from the original Hamming code 001101011. How do we find the 8th bit of the wrong code?
The algorithm is very simple. As long as we calculate it again on the algorithm that calculates the Hamming code check digit, we get the Hamming code check method, such as calculating the 2^k bit corresponding to 001101001.
1,3,5,7,9 XOR, get 0
X, 2, 3, 6, 7 XOR, get 0
X, 4, 5, 6, 7 XOR, get 0
8,9 XOR, get 1
We reverse the above results to get 1000, which is 8, in decimal. According to the Hamming code verification rule, the coding error is in the 8th position. We change the 0th digit of the 8th to 1 to get the original. Code 001101011.
The above example appears on the 2^k check digit. If it appears on the non-2^k bit, the result is the same, for example:
Suppose the received code is 001100011, that is, the sixth bit has an error, we follow the rules.
1,3,5,7,9 XOR, get 0
X, 2, 3, 6, 7 XOR, get 1
X, 4, 5, 6, 7 XOR, get 1
8,9 XOR, get 0
We reverse the above results to get 0110, which is 6 in decimal. According to the Hamming code verification rule, the coding error is in the sixth place. We change the 0th bit of the 6th to 1 to get the original. Code 001101011.
C++ implementation of encoding and verification of Hamming codeThrough the principle, we can easily realize the encoding and verification code of Hamming code.
Auto cal(size_t sz)-》decltype(auto)
{
Decltype(sz) k = 0;
Decltype(sz) cur = 1;
While (cur - 1 " sz + k )
{
Cur "" 1;
k++;
}
Return k;
}
Bool encode(const string &s, string &d)
{
D.clear();
Auto k = cal(s.size());
D.resize(s.size() + k);
For (decltype(d.size()) i = 0, j = 0, p = 0; i!= d.size();i++)
Decoding and verification:Auto antiCal(size_t sz)-"decltype(auto)
{
Decltype(sz) k = 0;
Decltype(sz) cur = 1;
While (cur " sz)
{
Cur "" 1;
k++;
}
Return k;
}
Auto decode(string &s, string &d)-"decltype(auto)
{
S.clear();
Auto k = antiCal(d.size());
S.resize(d.size() - k);
Decltype(d.size()) sum = 0;
For (decltype(k) p = 0; p != k;p++)
{
Int pAnti = 0;
Decltype(k) index = 1 "p;
For (decltype(d.size()) i = index - 1;i " d.size(); i+=index)
{
For (auto j = 0; j " index && i " d.size(); i++, j++)
pAnti ^= d[i] - '0';
}
Sum += pAnti "p;
}
If (sum != 0)
d[sum - 1] = (1- (int)(d[sum - 1] - '0')) + '0';
For (decltype(d.size()) i = 0, p = 0,j = 0; i != d.size(); i++)
{
If ((i + 1) == (1 "p) && p "k)
p++;
Else
s[j++] = d[i];
}
Return sum;
}
{
If ((i + 1) == pow(2,p) && p " k)
{
d[i] = '0';
p++;
}
Else if (s[j] == '0' || s[j] == '1')
d[i] = s[j++];
Else
Return false;
}
For (auto i = 0; i != k;i++)
{
Int count = 0 ,index = 1 "i;
For (auto j = index - 1; j " d.size() ;j += index)
For (auto k = 0; k!= index && j " d.size(); k++, j++)
Count ^= d[j] - '0';
d[index - 1] = '0' + count;
}
Return true;
}
Test sample:Int main()
{
String source, dest;
While (cin 》》 source)
{
If (encode(source,dest))
{
Cout ""Source:" "source" "endl;
Cout ""Dest: "" "dest" "endl;
}
Size_t index;
Cout ""----input error index : â€;
Cin 》》 index;
Auto k = dest.size();
If (index != 0 && index <<= dest.size())
Dest[index - 1] = (1 - (int)(dest[index - 1] - '0')) + '0';
Cout ""Code" "dest" "endl;
Auto ret = decode(source,dest);
If (ret == 0)
{
Cout ""Source:" "source" "endl;
Cout ""Dest: "" "dest" "endl;
}
Else
{
Cout ""Error index" "" ret "endl;
Cout ""Corret source: " "source "endl;
Cout ""Corret dest: " "dest" "endl;
}
Cout "endl;
}
Return 0;
}
Source: 10101
Dest: 001101011
----input error index : 8
Code 001101001
Error index 8
Corret source: 10101
Corret dest: 001101011
Source: 1001010101010101010111111001101
Dest: 1111001101010100101010101111110101101
----input error index : 20
Code 1111001101010100101110101111110101101
Error index 20
Corret source: 1001010101010101010111111001101
Corret dest: 1111001101010100101010101111110101101
Source: 1
Dest: 111
----input error index : 0
Code 111
Source: 1
Dest: 111
Fiber Optic Distribution Box,Fiber Optic Breakout Box,Fibre Optic Breakout Box,Fibre Break Out Box
Cixi Dani Plastic Products Co.,Ltd , https://www.dani-fiber-optic.com