The three-point oscillation circuit refers to an oscillation circuit where the three poles of the transistor (for AC signals) are directly connected to the three end points of the LC resonant circuit. The general structure of this circuit is shown in Figure Z0804. In the figure, X represents the reactance of each component constituting the resonant circuit.
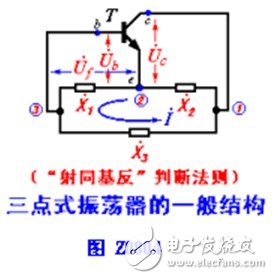
The resonant circuit is induced by two different types of reactance components of inductance and capacitance. At resonance, its equivalent impedance is purely resistive, so the total reactance must be zero, that is, X1 + X2 + X3 = 0, and The output voltage of the amplifier circuit (UC in the figure) is inverse to the input voltage (Ub in the figure), that is, φA = π. In order to satisfy the phase balance condition of oscillation, that is, φA + φF = 2nπ, φF = π is required, that is, the feedback network must have a phase shift of 180 °. Set the loop current to be obtained from Figure I0817

Obviously, φF = π can only be satisfied when X1 and X2 have the same sign, that is to say, X1 and X2 can only meet the phase balance condition when the reactance properties are the same (both inductance and capacitance). Because X1 + X2 + X3 = 0, the properties of X3 and X1 and X2 must be opposite, that is, if X1 and X2 are inductances, then X3 must be a capacitor.
In summary, the principle of forming a three-point oscillation circuit is that X1 and X2 have the same properties, and X3 has the opposite properties. It can be summarized as "the same as the base (collector) inverse", that is, the two reactive elements connected to the emitter have the same properties, and the two reactive elements connected to the base (or collector) have opposite properties. Using this principle, it can be quickly judged whether the three-point oscillation circuit satisfies the phase balance condition of oscillation.
A prism (Prism) is an optical element that deflects light according to a specific angle between the emitted light and the incident light. In the optical path, the prism has the function of changing the angle between the emitted light and the incident light (such as deflection 90°, 180°, etc.), shifting the light and changing the direction of the image. Prisms are widely used in laser research, laser optical systems, optical imaging, machine vision, life sciences, biomedicine and other fields or products. United Optics can provide a variety of prism stock standard products, such as K9 standard precision Right Angle Prism, K9 high precision right angle prism, UV fused silica standard precision right angle prism, UV fused silica high precision right angle prism, K9 pentagonal prism, K9 Dove prism, K9 roof prism, K9 corner reflector (K9 corner prism), ultraviolet fused silica corner reflector (ultraviolet fused silica corner prism), wedge prism, etc.
The "dispersive prism" that decomposes the composite light into the spectrum in the spectrometer, the more commonly used is the equilateral prism; in the periscope, binocular telescope and other instruments, the direction of the light is changed to adjust the imaging position of the "total reflection prism". ", generally right-angle prisms are used.
Irregular Prism,Special-Shaped Prism,Octagonal Prism,Mini Prism
Bohr Optics Co.,Ltd , https://www.bohr-optics.com