Decision tree is a basic classification and regression method. This paper mainly explains the decision tree used for classification. The decision tree is a tree structure that is classified according to relevant conditions. For example, the arrangement process of a high-end dating website meeting a female client's appointment object is a decision tree:
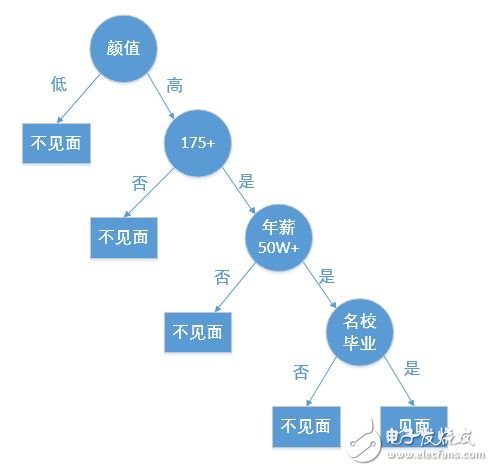
Creating a decision tree from a given data set is a machine learning course. Creating a decision tree can take more time, but using a decision tree is very fast.
The most critical question when creating a decision tree is which feature is selected as the classification feature. A good classification feature can maximize the separation of the data sets and turn the disorder into order. Here is a question, how to describe the degree of ordering a data set? In information theory and probability statistics, entropy represents the measure of the uncertainty of a random variable, that is, the degree of order.
Now give a set D, all the discussion in this article takes this set as an example:
Does the serial number not surfaced to survive? Is there an ankle?
1 yes yes yes
2 yes yes yes
3 Yes No No
4 no yes no
5 no yes no
The code to create the collection is as follows:
Def create_data_set():
dataSet = [[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']]
Labels = ['no surfacing', 'flippers'] #Do not surface or not, whether there are ankles
Return dataSet, labels
2.1 entropy (entropy)
The first contact of the blogger with the word "entropy" is in the chemistry class of high school, but it feels that the meaning of "entropy" in chemistry class is no different from the meaning in information theory. It is the degree of confusion, the greater the entropy. The more chaotic, such as the entropy of a cup of turbid water is greater than the entropy of a cup of pure water.
In information theory and probability statistics, let X be a discrete random variable with a finite number of values ​​whose probability distribution is:

Write a function that computes entropy, where dataSet is the data set that establishes the decision tree, with the last element of each row representing the category:
Def cal_Ent(dataSet): #calculate entropy from a given data set
Num = len(dataSet)
Labels = {}
For row in dataSet: #count the number of all tags
Label = row[-1]
If label not in labels.keys():
Labels[label] = 0
Labels[label] += 1
Ent = 0.0
For key in labels: #calculation entropy
Prob = float(labels[key]) / num
Ent -= prob * log(prob, 2)
Return Ent
2.2 information gain (informaTIon gain)
The information gain indicates the degree to which the information of the feature X is known such that the uncertainty of the information of the class Y is reduced.

When the probability in entropy and conditional entropy is estimated from the data, the corresponding entropy and conditional entropy are called empirical entropy and empirical condition entropy, respectively.
The decision tree selects a feature as the basis of its classification feature, that is, the feature has the greatest information gain for the set, that is, after the feature is removed, the set becomes the most ordered. Still taking the given set D as an example, the optimal classification feature is selected according to the calculated information gain criterion.
Expressed by X1, "Is it possible to survive without water?"

Write a function that selects the best decision feature, where dataSet is the data set that establishes the decision tree, and the last element of each row represents the category:
#分数æ®æ•°æ®é›† according to the given feature, return all the data whose value of the axis feature is value
Def split_data_set(dataSet, axis, value):
retDataSet = []
For row in dataSet:
If (row[axis]) == value:
reducedRow = row[:axis]
reducedRow.extend(row[axis+1:])
retDataSet.append(reducedRow)
Return retDataSet
#Select the best decision characteristics
Def choose_best_feature(dataSet):
Num = len(dataSet[0]) - 1 #Features
baseEnt = cal_Ent(dataSet)
besTInfoGain = 0.0
bestFeature = -1
For i in range(num):
Featlist = [example[i] for example in dataSet] #traverse the data set by column, select all values ​​of a feature
uniqueVals = set(featlist) #a value that a feature can take
newEnt = 0.0
For value in uniqueVals:
subDataSet = split_data_set(dataSet, i, value)
Prob = len(subDataSet) / float(len(dataSet))
newEnt += prob * cal_Ent(subDataSet)
infoGain = baseEnt - newEnt #Info gain
If (infoGain > besTInfoGain):
besTInfoGain = infoGain
bestFeature = i
Return bestFeature
The ID3 decision tree selects features based on information gain during the generation process.
2.3 information gain ratio (information gain ratio)
MW01 Smart Watch
Mw01 Smart Watch,Mw01 Smartwatch,Smart Watch Mw01,Smartwatch Mw01
everyone enjoys luck , https://www.eeluck.com