Editor's Note: Debarko De, a full-stack developer, introduced the concept of the capsule network in a concise manner, and also presented a capsule network implementation based on numpy and TensorFlow.
What is a capsule network? What is a capsule? Is the capsule network better than the Convolutional Neural Network (CNN)? This article will discuss these topics about the CapsNet (Capsule Network) proposed by Hinton.
Note that this is not a capsule in pharmacy, but a capsule in neural networks and machine learning.
Before reading this article, you need to have a basic understanding of CNN, otherwise you are advised to look at the Deep Learning for Noobs I wrote earlier. Below I will briefly review the knowledge of CNN related to this article, so that you can more easily understand the comparison between CNN and CapsNet below. Gossip is not much to say, let's get started.
Basically, CNN is a system of stacked bunches of neurons. CNN is very good at dealing with image classification problems. It is computationally expensive to have the neural network map all the pixels of an image. Convolution greatly simplifies calculations while preserving the nature of the data. Basically, convolution is a bunch of matrix multiplications, which are then added together.
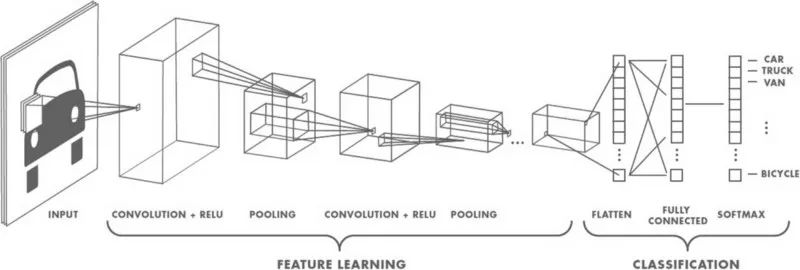
After the image is transmitted to the network, a set of cores or filters scans the image and performs a convolution operation to create a feature map. These features are then passed to the subsequent active and pooled layers. Depending on the number of layers in the network, this combination may be stacked repeatedly. Activating the network brings some non-linearity to the network (such as ReLU). Pooling (such as maximum pooling) helps reduce training time. The idea of ​​pooling is to create a "summary" for each sub-area. At the same time, pooling also provides some location and translation invariance for target detection. At the end of the network is a classifier, such as the softmax classifier, which returns the category. The training is backpropagated based on the error corresponding to the annotated data. In this step, nonlinearity helps solve the gradient attenuation problem.
What is wrong with CNN?
When classifying images that are very close to the dataset, CNN performed extremely well. But CNN performs poorly on images that are upside down, tilted, or otherwise oriented differently. Adding different variants of the same image during training can solve this problem. In CNN, each layer has a coarser understanding of the image. For example, suppose you are trying to classify boats and horses. The innermost layer (the first layer) understands the small curves and edges. The second layer may understand straight lines or small shapes, such as the curve of the ship's mast and the entire tail. The higher layers begin to understand more complex shapes, such as the entire tail or hull. The final layer attempts to get an overview of the full picture (eg the entire boat or the entire horse). We use pooling after each layer to complete the calculations in a reasonable amount of time, but essentially pooling also loses location information.
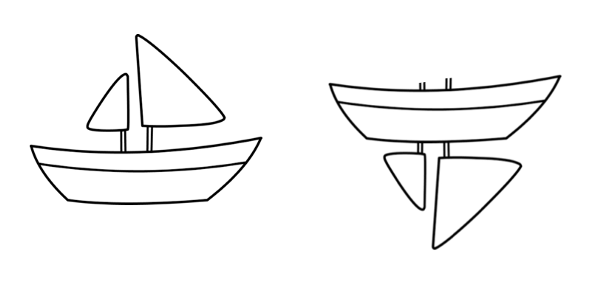
Malformation
Pooling helps to establish positional invariance. Otherwise CNN will only be able to fit images or data that are very close to the training set. Such invariance simultaneously results in images with ship parts but in the wrong order being mistaken for the ship. So the system will mistake the image on the right side of the picture above for the ship, and humans can clearly see the difference between the two. In addition, pooling also helps to establish proportional invariance.

Proportional invariance
Pooling was originally used to introduce position, orientation, and scale invariance, but this method is very rough. In fact, the pooling has added various positional invariances, so that the images with the wrong order of the parts are also mistaken for the ship. What we need is not invariance, but equivalence. Invariance allows CNN to tolerate small changes in the perspective, while equivalence allows CNN to understand orientation and scale changes and adapt the image accordingly so that the spatial position information of the image is not lost. CNN will reduce its size to detect smaller ships. This led to the recently developed capsule network.
What is a capsule network?
Sara Sabour, Nicholas Frost, and Geoffrey Hinton published the paper Dynamic Routing Between Capsules in October 2017. When Geoffrey Hinton, one of the grandparents of deep learning, published a paper, the paper is destined to be a major breakthrough. The entire deep learning community is crazy about this. This paper discusses capsules, capsule networks, and experiments on MNIST. MNIST is an annotated handwritten digital image data set. Compared to the current state-of-the-art CNN, the performance of the capsule network on overlapping numbers has improved significantly. The authors of the paper suggest that the human brain has a module called “capsules†that are particularly good at handling different visual stimuli, as well as coding poses (position, size, orientation), deformation, velocity, reflectivity, hue, texture, etc. . The brain must have the mechanism to "route" low-level visual information to the capsule that is best at handling that information.
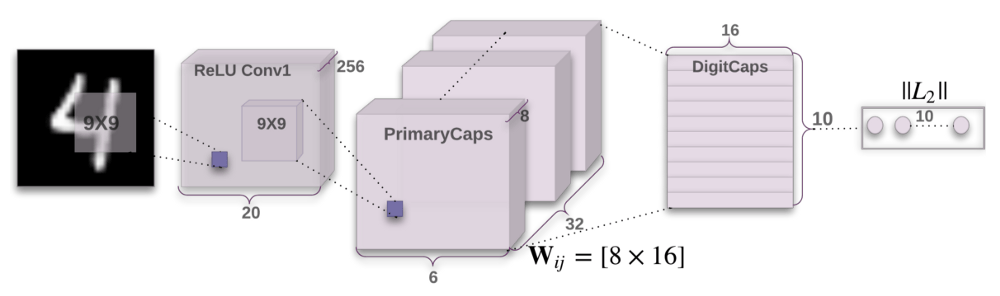
Capsule network architecture
A capsule is a set of nested neural network layers. In the usual neural network, you are constantly adding more layers. In a capsule network, you add more layers to a single network layer. In other words, nesting another one in one neural network layer. The state of the neurons in the capsule characterizes the above attributes of an entity in the image. The capsule outputs a vector representing the existence of the entity. The orientation of the vector represents the attributes of the entity. The vector is sent to all possible parent capsules in the neural network. The capsule can calculate a prediction vector for each possible parent, and the prediction vector is obtained by multiplying its weight by the weight matrix. The association of the parent capsule with the largest predicted vector product scalar will be enhanced, while the remaining parent capsule contact will be weakened. This desiry-based routing approach is superior to existing mechanisms such as maximum pooling. The maximum pooled routing is based on the most intense features detected by the lower layer network. In addition to dynamic routing, the capsule network adds a squash function to the capsule. Squash is a nonlinear function. Unlike CNN adding squash functions to each network layer, the capsule network adds squash functions to each set of nested network layers, applying the squash function to the output vector of each capsule.
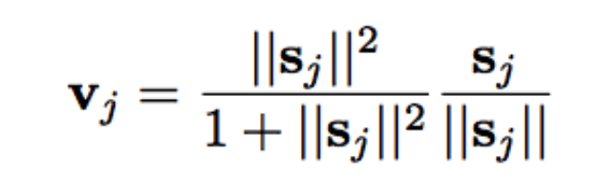
The paper introduces a new squash function (see above). ReLU and similar nonlinear functions performed well on a single neuron, but the paper found that the squash function performed best on the capsule. The squash function compresses the length of the output vector of the capsule: when the vector is small, the result is 0; when the vector is large, the result is 1. Dynamic routing adds some extra computational overhead, but it undoubtedly brings advantages.
Of course, we must also note that the concept of capsules has not been fully tested since the paper was published. It performed well on the MNIST dataset, but performance on other, more diverse data sets remains to be proven. Within a few days of the publication of the paper, some people made some comments.
There is room for improvement in current capsule network implementations. But don't forget that Hinton's paper was mentioned at the beginning:
The goal of this paper is not to explore the entire space, but to simply show that a fairly straightforward implementation performs well, while dynamic routing benefits.
Ok, we have already talked enough about the theory. Let's have some fun and build a capsule network. I will lead you through some code that configures a capsule network for MNIST data. I will add comments to the code so that you can understand how the code works from line to line. This article will include two important code snippets. The rest of the code is in the GitHub repository:
# only rely on numpy and tensorflow
Import numpy as np
Import tensorflow as tf
From config import cfg
# Define convolution capsules, which are composed of multiple neural network layers
#
classCapsConv(object):
''' Capsule layer
parameter:
Input: A 4-dimensional tensor.
Num_units: integer, the length of the output vector of the capsule.
With_routing: Boolean value, the capsule is routed through the lower layer capsule.
Num_outputs: The number of capsules in this layer.
return:
A 4D tensor.
'''
Def __init__(self, num_units, with_routing=True):
Self.num_units = num_units
Self.with_routing = with_routing
Def __call__(self, input, num_outputs, kernel_size=None, stride=None):
Self.num_outputs = num_outputs
Self.kernel_size = kernel_size
Self.stride = stride
Ifnot self.with_routing:
#Primary Caps layer
# Enter: [batch_size, 20, 20, 256]
Assert input.get_shape() == [cfg.batch_size, 20, 20, 256]
Capsules = []
For i in range(self.num_units):
# Each capsule i: [batch_size, 6, 6, 32]
With tf.variable_scope('ConvUnit_' + str(i)):
Caps_i = tf.contrib.layers.conv2d(input,
Self.num_outputs,
Self.kernel_size,
Self.stride,
Padding="VALID")
Caps_i = tf.reshape(caps_i, shape=(cfg.batch_size, -1, 1, 1))
Capsules.append(caps_i)
Assert capsules[0].get_shape() == [cfg.batch_size, 1152, 1, 1]
# [batch_size, 1152, 8, 1]
Capsules = tf.concat(capsules, axis=2)
Capsules = squash(capsules)
Assert capsules.get_shape() == [cfg.batch_size, 1152, 8, 1]
Else:
#æ•°å—胶囊(DigitCaps) layer
# reshapeInput to: [batch_size, 1152, 8, 1]
Self.input = tf.reshape(input, shape=(cfg.batch_size, 1152, 8, 1))
# b_IJ: [1, num_caps_l, num_caps_l_plus_1, 1]
b_IJ = tf.zeros(shape=[1, 1152, 10, 1], dtype=np.float32)
Capsules = []
For j in range(self.num_outputs):
With tf.variable_scope('caps_' + str(j)):
Caps_j, b_IJ = capsule(input, b_IJ, j)
Capsules.append(caps_j)
# Return a tensor: [atch_size, 10, 16, 1]
Capsules = tf.concat(capsules, axis=1)
Assert capsules.get_shape() == [cfg.batch_size, 10, 16, 1]
Return(capsules)
Def capsule(input, b_IJ, idx_j):
''' Routing algorithm for a single capsule in layer l+1.
parameter:
Input: tensor [batch_size, num_caps_l=1152, length(u_i)=8, 1]
Num_caps_l is the number of capsules in layer l
return:
Tensor [batch_size, 1, length(v_j)=16, 1]
l+1 layer capsule j output vector `v_j`
note:
U_i represents the output vector of the layer 1 capsule i,
V_j represents the output vector of the l+1 layer capsule j
'''
With tf.variable_scope('routing'):
W_initializer = np.random.normal(size=[1, 1152, 8, 16], scale=0.01)
W_Ij = tf.Variable(w_initializer, dtype=tf.float32)
# Repeat batch_size times W_Ij:[batch_size, 1152, 8, 16]
W_Ij = tf.tile(W_Ij, [cfg.batch_size, 1, 1, 1])
#计算u_hat
# [8, 16].T x [8, 1] => [16, 1] => [batch_size, 1152, 16, 1]
U_hat = tf.matmul(W_Ij, input, transpose_a=True)
Assert u_hat.get_shape() == [cfg.batch_size, 1152, 16, 1]
Shape = b_IJ.get_shape().as_list()
Size_splits = [idx_j, 1, shape[2] - idx_j - 1]
For r_iter in range(cfg.iter_routing):
#第4线:
# [1, 1152, 10, 1]
c_IJ = tf.nn.softmax(b_IJ, dim=2)
Assert c_IJ.get_shape() == [1, 1152, 10, 1]
#第5线:
# in the third dimension using c_I weighted u_hat
# Then in the second dimension, get [batch_size, 1, 16, 1]
b_Il, b_Ij, b_Ir = tf.split(b_IJ, size_splits, axis=2)
c_Il, c_Ij, b_Ir = tf.split(c_IJ, size_splits, axis=2)
Assert c_Ij.get_shape() == [1, 1152, 1, 1]
S_j = tf.multiply(c_Ij, u_hat)
S_j = tf.reduce_sum(tf.multiply(c_Ij, u_hat),
Axis=1, keep_dims=True)
Assert s_j.get_shape() == [cfg.batch_size, 1, 16, 1]
#å…è¡Œ:
# Using the squash function mentioned above, get: [batch_size, 1, 16, 1]
V_j = squash(s_j)
Assert s_j.get_shape() == [cfg.batch_size, 1, 16, 1]
#第7行:
#平铺v_j, from [batch_size , 1, 16, 1] to [batch_size, 1152, 16, 1]
# [16, 1].T x [16, 1] => [1, 1]
# Then recursively the mean in the batch_size dimension to get [1, 1152, 1, 1]
V_j_tiled = tf.tile(v_j, [1, 1152, 1, 1])
U_produce_v = tf.matmul(u_hat, v_j_tiled, transpose_a=True)
Assert u_produce_v.get_shape() == [cfg.batch_size, 1152, 1, 1]
b_Ij += tf.reduce_sum(u_produce_v, axis=0, keep_dims=True)
b_IJ = tf.concat([b_Il, b_Ij, b_Ir], axis=2)
Return(v_j, b_IJ)
Def squash(vector):
'''compression function
parameter:
Vector: a 4-dimensional tensor [batch_size, num_caps, vec_len, 1],
return:
a 4-dimensional tensor of the same shape as the vector,
But the 3rd and 4th dimensions are compressed
'''
Vec_abs = tf.sqrt(tf.reduce_sum(tf.square(vector))) #a scalar
Scalar_factor = tf.square(vec_abs) / (1 + tf.square(vec_abs))
Vec_squashed = scalar_factor * tf.divide(vector, vec_abs) # Multiply the corresponding elements
Return(vec_squashed)
Above is a whole capsule layer. The capsule layers are stacked to form a capsule network.
Import tensorflow as tf
From config import cfg
From utils import get_batch_data
From capsLayer importCapsConv
classCapsNet(object):
Def __init__(self, is_training=True):
Self.graph = tf.Graph()
With self.graph.as_default():
If is_training:
self.X, self.Y = get_batch_data()
Self.build_arch()
Self.loss()
# t_vars = tf.trainable_variables()
Self.optimizer = tf.train.AdamOptimizer()
Self.global_step = tf.Variable(0, name='global_step', trainable=False)
Self.train_op = self.optimizer.minimize(self.total_loss, global_step=self.global_step) # var_list=t_vars)
Else:
self.X = tf.placeholder(tf.float32,
Shape=(cfg.batch_size, 28, 28, 1))
Self.build_arch()
Tf.logging.info('Seting up the main structure')
Def build_arch(self):
With tf.variable_scope('Conv1_layer'):
# Conv1(第一å·å±‚), [batch_size, 20, 20, 256]
Conv1 = tf.contrib.layers.conv2d(self.X, num_outputs=256,
Kernel_size=9, stride=1,
Padding='VALID')
Assert conv1.get_shape() == [cfg.batch_size, 20, 20, 256]
# TODO: Rewrite the 'CapsConv' class as a function,
# capsLay function should be packaged as two functions,
# One is similar to conv2d and the other is fully_connected (full connection) of TensorFlow.
#主胶囊,[batch_size, 1152, 8, 1]
With tf.variable_scope('PrimaryCaps_layer'):
primaryCaps = CapsConv(num_units=8, with_routing=False)
Caps1 = primaryCaps(conv1, num_outputs=32, kernel_size=9, stride=2)
Assert caps1.get_shape() == [cfg.batch_size, 1152, 8, 1]
#æ•°å—胶囊层,[batch_size, 10, 16, 1]
With tf.variable_scope('DigitCaps_layer'):
digitCaps = CapsConv(num_units=16, with_routing=True)
Self.caps2 = digitCaps(caps1, num_outputs=10)
# encoder structure in the previous diagram
# 1. Mask:
With tf.variable_scope('Masking'):
# a). Calculate ||v_c||, then calculate softmax(||v_c||)
# [batch_size, 10, 16, 1] => [batch_size, 10, 1, 1]
Self.v_length = tf.sqrt(tf.reduce_sum(tf.square(self.caps2),
Axis=2, keep_dims=True))
Self.softmax_v = tf.nn.softmax(self.v_length, dim=1)
Assert self.softmax_v.get_shape() == [cfg.batch_size, 10, 1, 1]
# b). Select the index of the maximum softmax value of 10 capsules
# [batch_size, 10, 1, 1] => [batch_size] (index)
Argmax_idx = tf.argmax(self.softmax_v, axis=1, output_type=tf.int32)
Assert argmax_idx.get_shape() == [cfg.batch_size, 1, 1]
# c). Index
# Since we are 3D creatures,
# Understanding the indexing process of argmax_idx is not easy
Masked_v = []
Argmax_idx = tf.reshape(argmax_idx, shape=(cfg.batch_size, ))
For batch_size in range(cfg.batch_size):
v = self.caps2[batch_size][argmax_idx[batch_size], :]
Masked_v.append(tf.reshape(v, shape=(1, 1, 16, 1)))
Self.masked_v = tf.concat(masked_v, axis=0)
Assert self.masked_v.get_shape() == [cfg.batch_size, 1, 16, 1]
# 2. Rebuilding MNIST images using 3 fully connected layers
# [batch_size, 1, 16, 1] => [batch_size, 16] => [batch_size, 512]
With tf.variable_scope('Decoder'):
Vector_j = tf.reshape(self.masked_v, shape=(cfg.batch_size, -1))
Fc1 = tf.contrib.layers.fully_connected(vector_j, num_outputs=512)
Assert fc1.get_shape() == [cfg.batch_size, 512]
Fc2 = tf.contrib.layers.fully_connected(fc1, num_outputs=1024)
Assert fc2.get_shape() == [cfg.batch_size, 1024]
Self.decoded = tf.contrib.layers.fully_connected(fc2, num_outputs=784, activation_fn=tf.sigmoid)
Def loss(self):
# 1. Marginal loss
# [batch_size, 10, 1, 1]
# max_l = max(0, m_plus-||v_c||)^2
Max_l = tf.square(tf.maximum(0., cfg.m_plus - self.v_length))
# max_r = max(0, ||v_c||-m_minus)^2
Max_r = tf.square(tf.maximum(0., self.v_length - cfg.m_minus))
Assert max_l.get_shape() == [cfg.batch_size, 10, 1, 1]
# reshape: [batch_size, 10, 1, 1] => [batch_size, 10]
Max_l = tf.reshape(max_l, shape=(cfg.batch_size, -1))
Max_r = tf.reshape(max_r, shape=(cfg.batch_size, -1))
#ç®—T_c: [batch_size, 10]
# T_c = Y, is my understanding correct? Give it a try.
T_c = self.Y
# [batch_size, 10], multiply the corresponding elements
L_c = T_c * max_l + cfg.lambda_val * (1 - T_c) * max_r
Self.margin_loss = tf.reduce_mean(tf.reduce_sum(L_c, axis=1))
# 2. Rebuild the loss
Orgin = tf.reshape(self.X, shape=(cfg.batch_size, -1))
Squared = tf.square(self.decoded - orgin)
Self.reconstruction_err = tf.reduce_mean(squared)
# 3. Total loss
Self.total_loss = self.margin_loss + 0.0005 * self.reconstruction_err
# to sum up
Tf.summary.scalar('margin_loss', self.margin_loss)
Tf.summary.scalar('reconstruction_loss', self.reconstruction_err)
Tf.summary.scalar('total_loss', self.total_loss)
Recon_img = tf.reshape(self.decoded, shape=(cfg.batch_size, 28, 28, 1))
Tf.summary.image('reconstruction_img', recon_img)
Self.merged_sum = tf.summary.merge_all()
The complete code (with training and validation models) can be found here (https://github.com/debarko/CapsNet-Tensorflow). The code is released under the Apache 2.0 license. I refer to the code of naturomics (https://github.com/naturomics).
to sum up
We introduced the concept of a capsule network and how to implement a capsule network. We try to understand that the capsule is a high-level nested neural network layer. We also looked at how the capsule network delivers orientation and other invariance—the equivalence of maintaining spatial configuration for each entity in the image. I am convinced that there are some questions that are not answered in this article, the most important of which is probably the capsule and its best implementation. However, this article is a preliminary attempt to explain this topic. If you have any questions, please comment. I will do my best to answer.
Siraj Raval and his speech have had a great impact on this article. Please share this article on Twitter. Follow me on twitter to get updates in the future.
24v power supply, the current range is 2A-9.2A, the max power is 220w. We also can meet your specific requirement of the prodcuts.The material of this product is PC+ABS. All condition of our product is 100% brand new.
Our products built with input/output overvoltage protection, input/output overcurrent protection, over temperature protection, over power protection and short circuit protection. You can send more details of this product, so that we can offer best service to you!
24V Power Supply,24V Pc Power Supply,24V Dc Power Supply ,24V Power Supply For Pc
Shenzhen Waweis Technology Co., Ltd. , https://www.waweispowerasdapter.com